atan2()
atan2() es una función que toma dos coordenadas (primero la Y y después la X) y devuelve el angulo que hace ese punto con el origen (0,0) de ese sistema coordenado. es una adaptación de la función arcotangente evitando los valores indefinidos típicos de esta en 𝛑/2 y 3𝛑/2.
veamos el video correspondiente:
funciones seno y coseno
para entender la función atan2() debemos recordar algunos conceptos básicos de trigonometría.
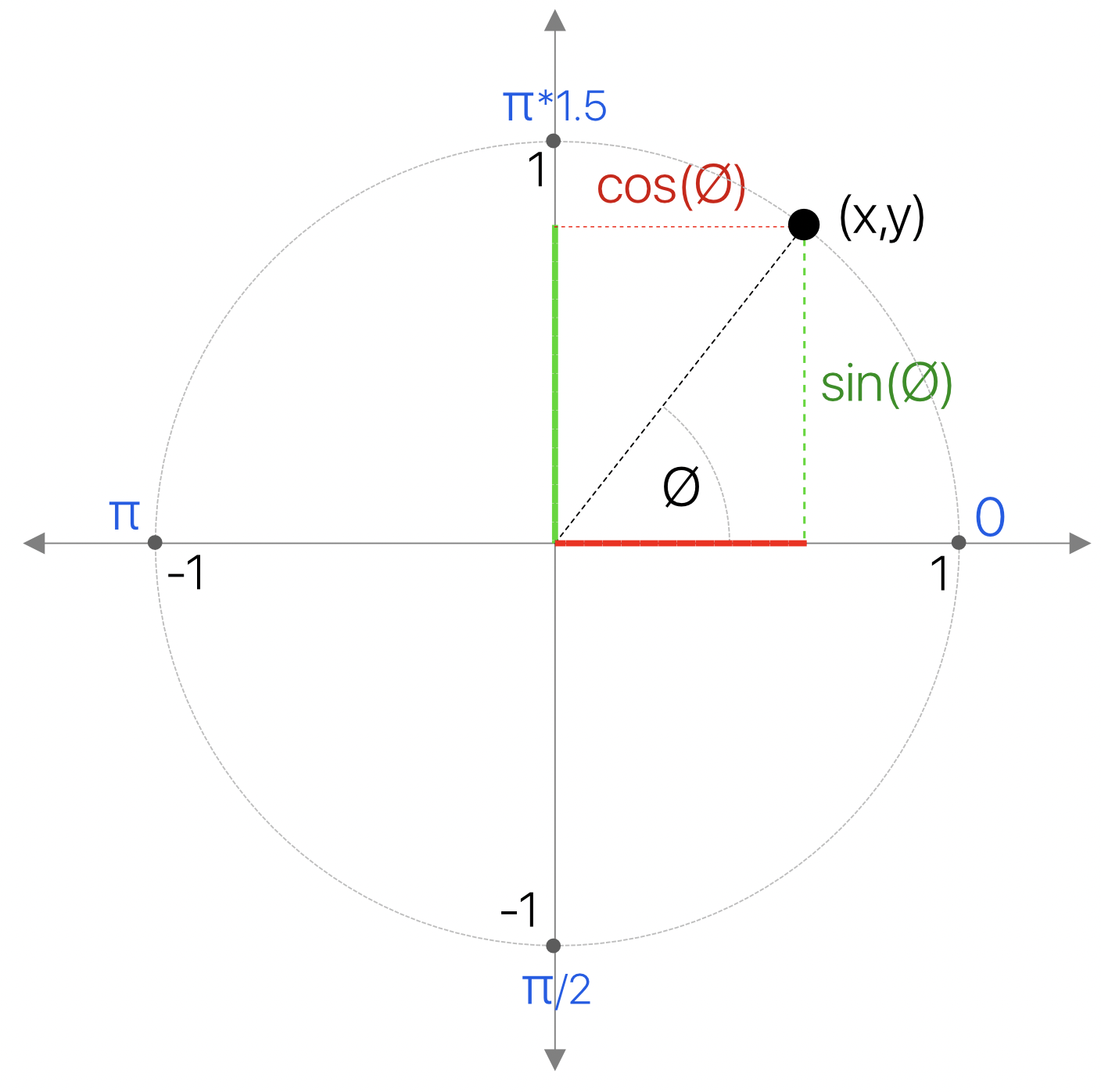
como sabemos las funciones trigonométricas seno y coseno se define en geometría polar como el cateto opuesto y el cateto adyacente del círculo unitario (un círculo imaginario con su centro en 0,0 y con radio igual a la unidad):
tangente()
por otro lado la función tangente puede ser definida como tan(𝜽) = sin(𝜽)/cos(𝜽), que en tomando en cuenta lo expresado arriba podría estar expresada como tan(𝜽) = y/x:
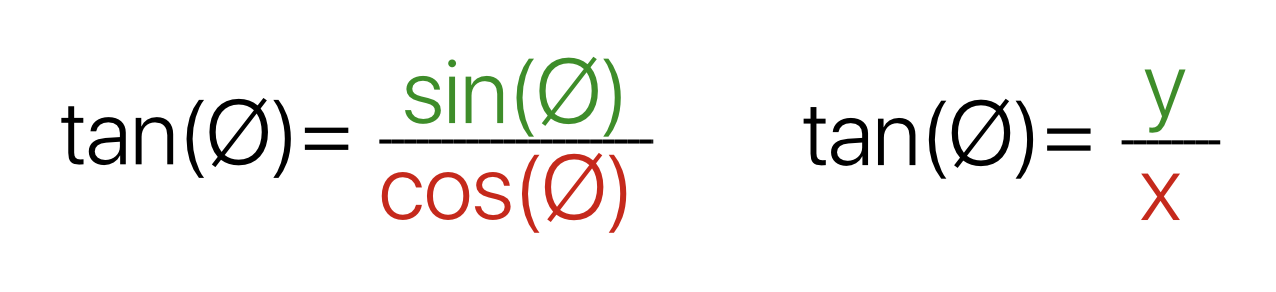
la función atan(x,y)
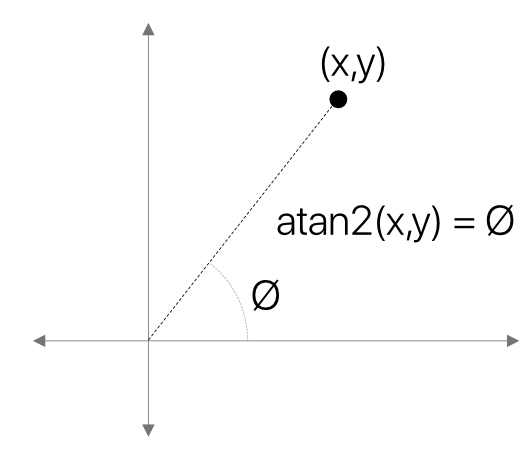
con la función tangente definida como tan(𝜽) = y/x, permite abrir la posibilidad de definir su inversa atan2(x,y), como una función que toma las dos coordenadas (primero la Y y después la X) y devuelve el angulo que hace ese punto con el origen (0,0) de ese sistema coordenado. en otras palabras, es una adaptación de la función arcotangente pero evitando los valores indefinidos típicos de esta en 𝛑/2 y 3𝛑/2.
atan2(y,x) apareció por primera vez en el lenguaje de programación FORTRAN, más especificamente en la implementación de IBM FORTRAN-IV en 1961.
esta función se puede definir como la conversión de un par ordenado (x,y) que está en coordenadas cartesianas al par (r,𝜽) en coordenadas polares; devolviendo valores en el ámbito [-𝛑,𝛑].
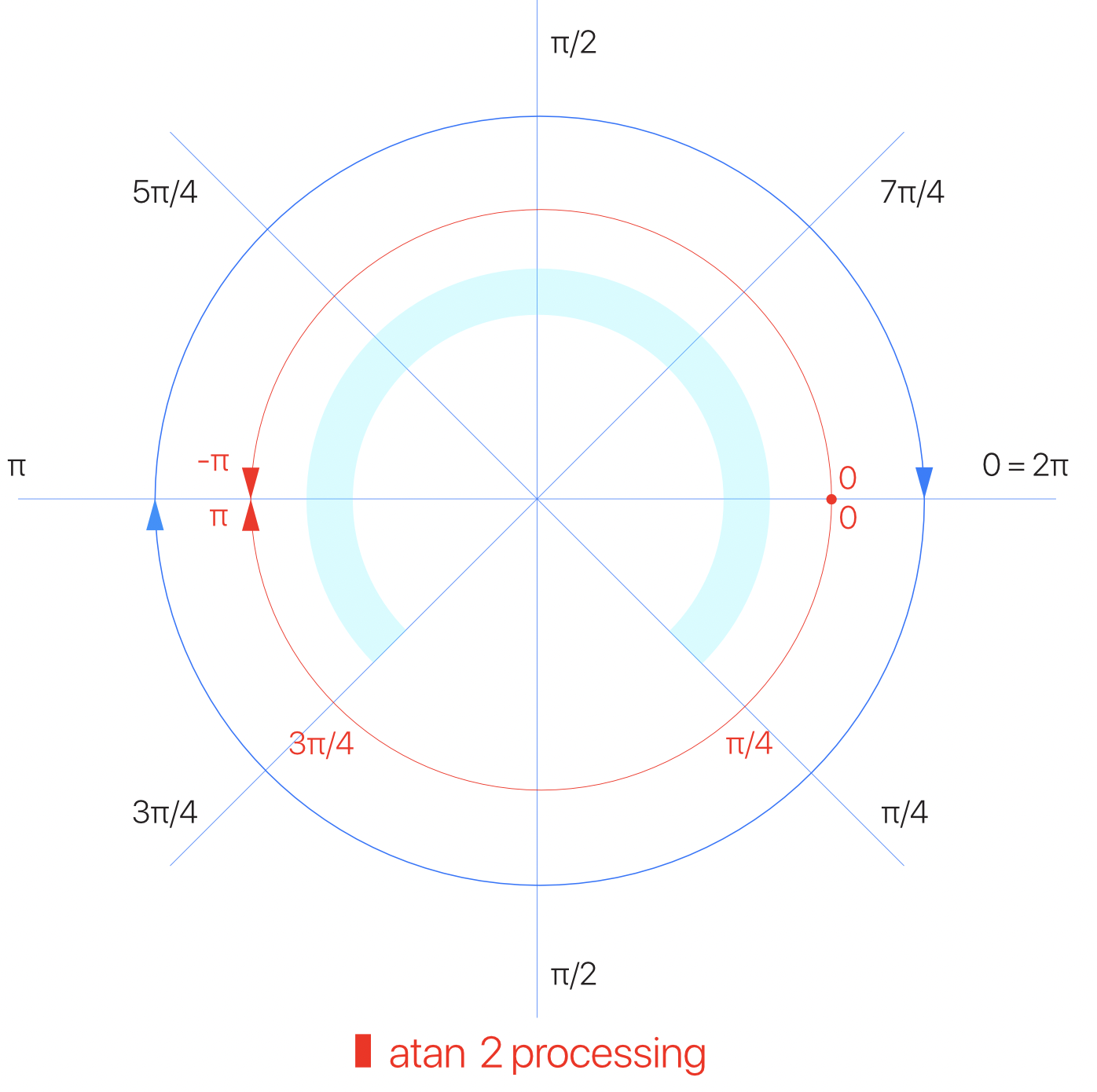
para usar esta función es muy importante tomar en cuenta que los radians en processing empiezan con el cero a la derecha y van aumentando a favor de las manecillas del reloj, como se ve en esta gráfica:
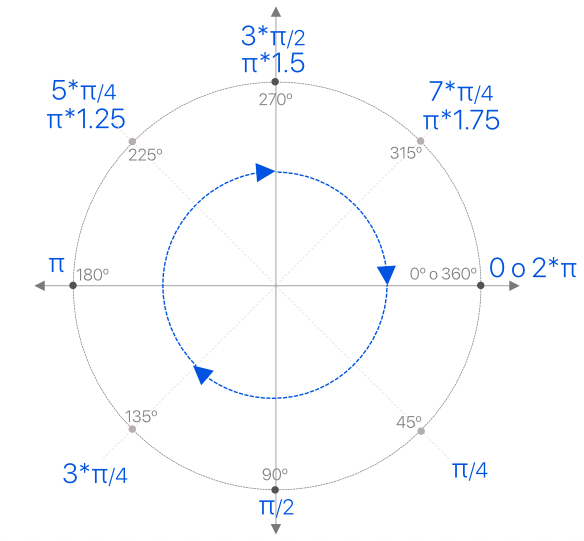
sin embargo, los resultados de la función atan2() en processing se dan en forma distinta:
los resultados positivos entre [0,𝛑] se dan empezando en el mismo 0 del lado derecho a favor de las manecillas del reloj, y a partir de 𝛑 al continuar hacia arriba los resultado obtenido van de [-𝛑,0]: